
Further, gradient descent is also used to train Neural Networks. Gradient Descent is known as one of the most commonly used optimization algorithms to train machine learning models by means of minimizing errors between actual and expected results.
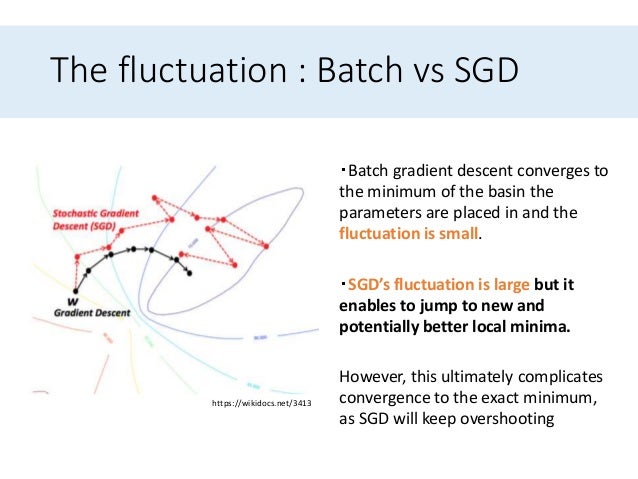
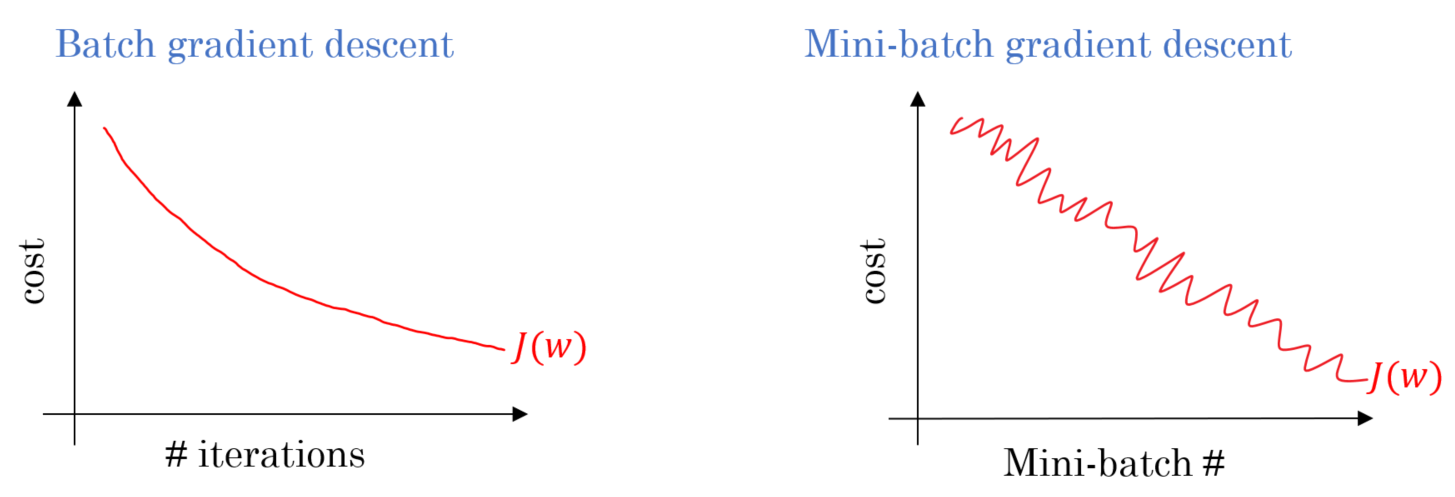
But what happens if we chose to set the number of batches to 1 or equal to the number of training examples? Batch Gradient DescentĪs stated before, in this gradient descent, each batch is equal to the entire dataset.Next → ← prev Gradient Descent in Machine Learning To prepare the mini-batches, one most apply some preprocessing steps: randomizing the dataset to randomly split the dataset and then partitioning it in the right number of chunks. parameters = update_parameters(parameters, grads) grads = backward_propagation(a, caches, parameters) # Update parameters. cost += compute_cost(a, Y) # Backward propagation. X = data_input Y = labels parameters = initialize_parameters(layers_dims) for i in range(0, num_iterations): minibatches = random_mini_batches(X, Y, mini_batch_size) for minibatch in minibatches: # Select a minibatch (minibatch_X, minibatch_Y) = minibatch # Forward propagation a, caches = forward_propagation(X, parameters) # Compute cost. Most of the projects use Mini-batch GD because it is faster in larger datasets. This allows us to move quickly to the global minimum in the cost function and update the weights and biases multiple times per epoch now. So instead of waiting until the algorithm runs through the entire dataset to only after update the weights and bias, it updates at the end of each, so-called, mini-batch. Imagine taking your dataset and dividing it into several chunks, or batches. Although it provides stable convergence and a stable error, this method uses the entire training set hence it is very slow for big datasets. In this method, every epoch runs through all the training dataset, to only then calculate the loss and update the W and b values. This classic Gradient Descent is also called Batch Gradient Descent. For a more deep approach to Forward and Backward Propagation, Compute Losses, Gradient Descent, check this post.
We also multiply this gradient to a learning rate alpha, which controls how big the step would be. In other words, the new weight/bias value will be the last one minus the gradient, moving it close to the global minimum value of the cost function. We are now ready to update the weight matrix W and the bias vector b. The Backward Propagation step is calculated using derivatives and return the “gradients”, values that tell us in which direction we should follow to minimize the cost function. And this part is called, as you may anticipate, Backward Propagation. With this error, we can now propagate it backward, updating every weight and bias and trying to minimize this error. Once we have an output, we compare this output with the expected output and calculate how far it is from each other, the error. This first pass is one of the main steps when calculating Gradient Descent and it is called Forward Propagation. Reviewing this quickly, before we can compute the GD, first the inputs are taken and passed through all the nodes of a neural network, calculating the weighted sum of inputs, weights, and bias. Source: Stanford’s Andrew Ng’s MOOC Machine Learning Course Minimizing the Cost Function, a Gradient Descent Illustration. It iteratively updates the weights and bias trying to reach the global minimum in a cost function. The Gradient Descent (GD) is an algorithm to minimize the cost function J(W,b) in each step. One of the most common algorithms that help the NN to reach the correct values of weights and bias. After some time training the network, these patterns are learned and we have a set of weights and biases that hopefully correct classifies the inputs. The acting of tuning is done through the optimization algorithms, the amazing feature that allows NN to learn. We can make an analogy with these concepts with the memory in which a NN stores patterns, and it is through tuning these parameters that we teach a NN.
Should I use Batch Gradient Descent? Mini-batch Gradient Descent or Stochastic Gradient Descent? In this post, we are going to understand the difference between those concepts and take a look at code implementations from Gradient Descent, to clarify these methods.Īt this point, we know that our matrix of weights W and our vector of bias b are the core values of our Neural Networks (NN) (Check the Deep Learning Basics post). One of the main questions that arise when studying Machine Learning and Deep Learning is the several types of Gradient Descent. Batch vs Mini-batch vs Stochastic Gradient Descent with Code Examples


 0 kommentar(er)
0 kommentar(er)
